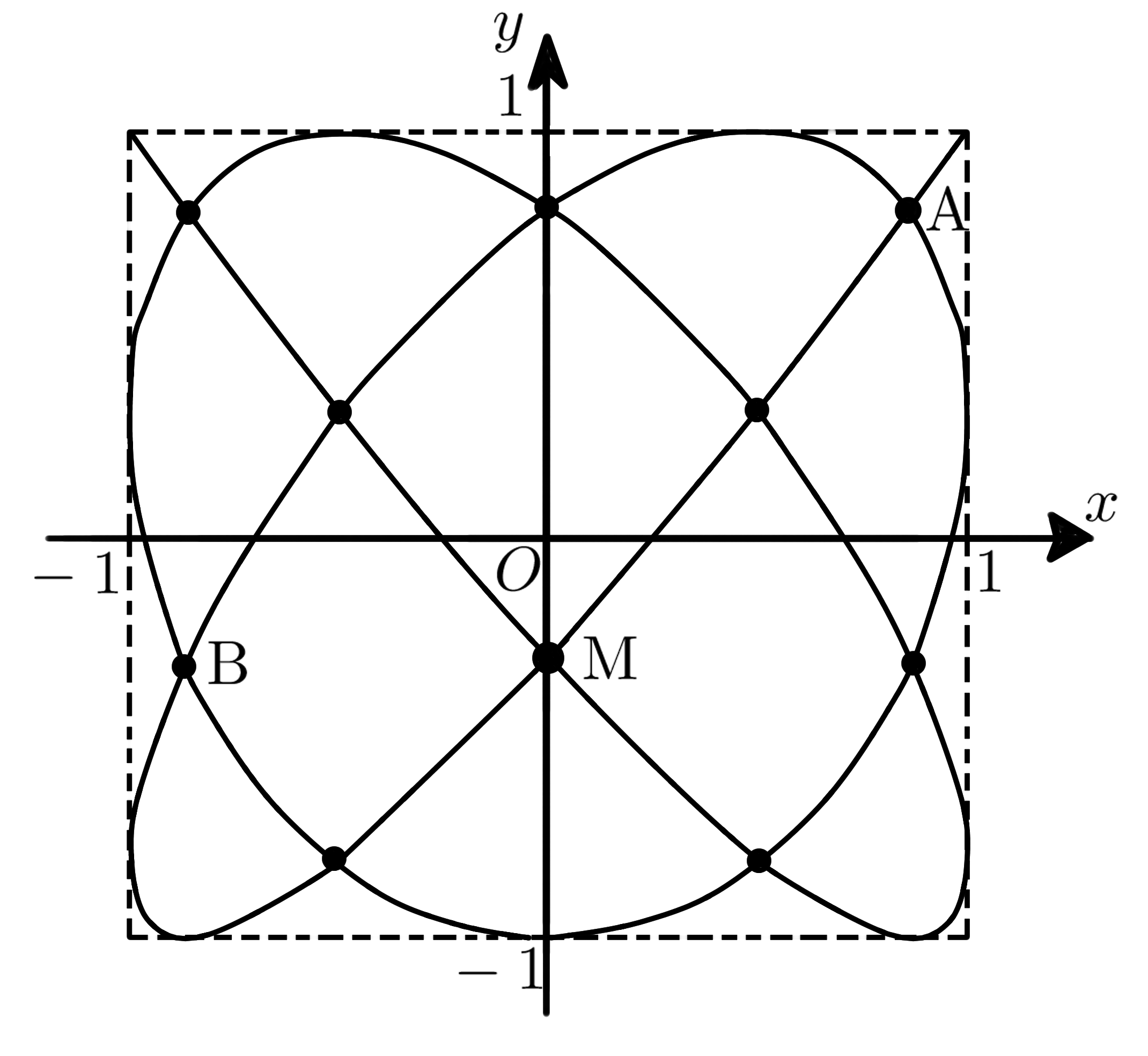
時刻$\;t\;$における座標が$$x = \cos 5t,\; y = \cos 6t \qquad (0 \leqq t \leqq \pi)$$で表される座標平面上の点$\; \mathrm{P}\;$の運動を考える。点$\; \mathrm{P} \;$がえがく曲線を$\;C\;$とする。曲線$\;C\;$の概形は下図のようになり，$\;t\;$が$\;0 \leqq t \leqq \pi\;$の範囲で動くとき点$\; \mathrm{P}\;$が2回通過する点は10個ある。そのうち3点$\; \mathrm{A, B, M}\;$を下図のようにとる。$\;\displaystyle \cos \frac{\pi}{5} = \frac{\sqrt{5} + 1}{4}\;$を用いて，以下の問いに答えよ。
(配点 50)
(i) 点$\; \mathrm{M}\;$は$\;y\;$軸上の$\;y \lt 0\;$の部分にある。点$\; \mathrm{M}\;$の$\;y\;$座標を，有理数$\; a, b\;$を用いて$\; a + b\sqrt{5}\;$の形で表せ。
(ii) $\; 0 \leqq t \leqq \pi\;$の範囲で次の方程式を解け。$$\cos 6t = \cos \frac{\pi}{5}$$
(iii) $\; \alpha_1 = \displaystyle{\frac{\pi}{30}}\;$とする。$\; t = \alpha_1\;$のとき，$\; (\cos 5\alpha_1, \; \cos 6\alpha_1)\;$は点$\; \mathrm{A}\;$である。$\; \alpha_1 \lt \alpha_2 \lt \pi\;$をみたすある値$\; \alpha_2\;$について，$\; t = \alpha_2\;$のときも$\; (\cos 5\alpha_2,\; \cos 6\alpha_2)\;$が点$\; \mathrm{A}\;$となる。この値$\; \alpha_2\;$を求めよ。
(iv) 点$\; \mathrm{M}\;$と第3象限の点$\; \mathrm{B}\;$は$\; y\;$座標が等しい。点$\; \mathrm{B}\;$の$\; x\;$座標を求めよ。また，直線$\; \mathrm{AB}\;$の方程式を，実数$\; m, n\;$を用いて$\; y= mx + n\;$の形で表せ。
